Title: Combinatorial Game Theory Applying Go Endgames
Speaker: Takenobu Takizawa
Abstract
Professor Berlekamp and his research group started to apply Combinatorial Game Theory to mathematical Go endgames in the 1990s. The author joined the group around 1991. We studied small-area (room) analysis without kos and with kos. Small-area analysis without kos is relatively easy.
!. Example without kos
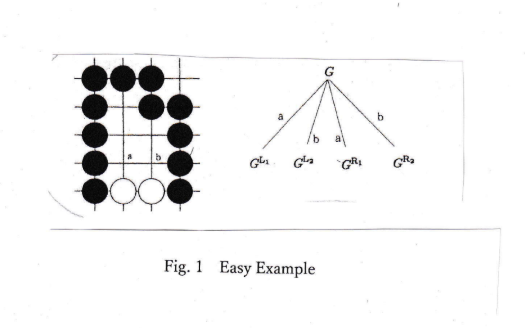
Fig.1 shows an easy example of endgame of Go. Both Black and White may play a or b.
The outcome of chilled game of G is G-1. G*1 is defined by Y{ G^L-1 I G^R +1 Y}.
-1 or + 1 is TAX for white (black) because it is usually get one point each for one move in end
stage of Endgame of Go. Under this hypothesis, Fig 1 is analyzed that
G.L=¥{2+1/8,2+up 13/4,1/2¥}=¥{2+1/811/2¥}=1+1/4.
2. Simple 1-point ko
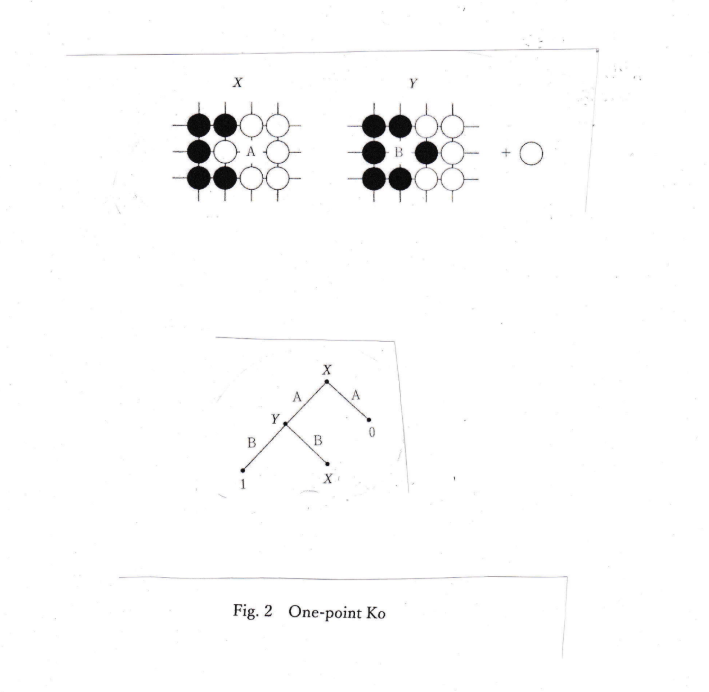
Fig.2 shows a simple 1-point ko. If Black’s turn, he may play the ko and take a stone.
White may not take back the ko immediately. If White plays another place X and Black
responds there, then White may take back the ko. X is called a ko-threat.
3. Ko-master
When there is a ko, Black or White eventually filles the ko. The filling side is the winner
of the ko and cailed ko-master. Note that ko-master must fill the ko.
4. Hidden Ko position
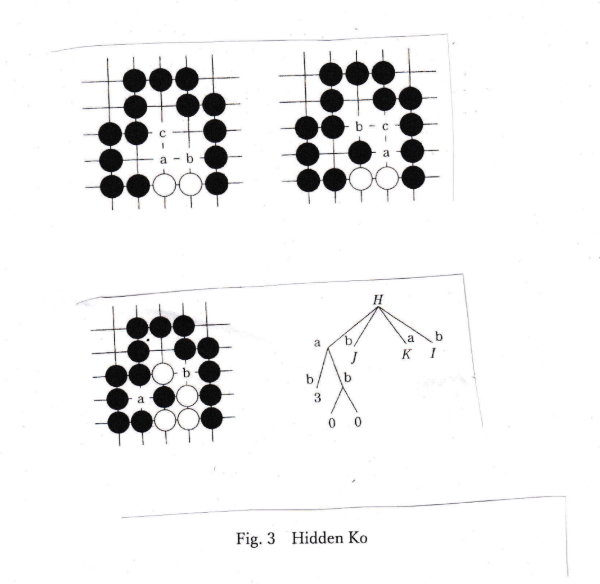
Fig. 3 shows a hidden-ko. There are no kos. But, after couple of plays, there might be a
ko. Thie type of ko is calied hidden ko.
5. Rogue Positions
There are interesting positions called Rogue Positions including hidden Ko
5.1 Wolfe’s Rogue posirion
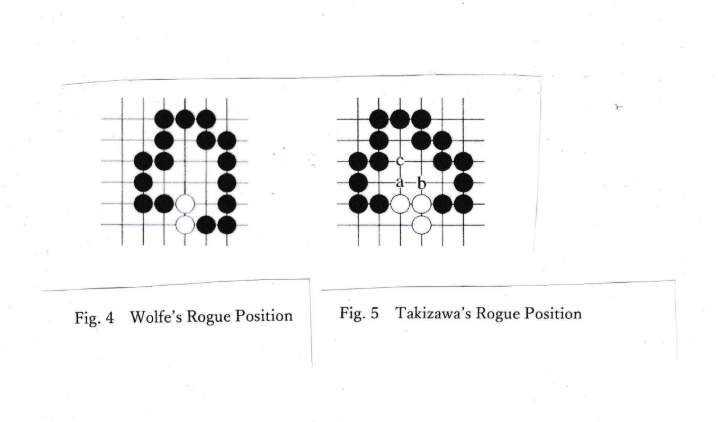
Fig.4 shows Wolfe’S Rogue position.
5.2 Takizawa’s Rogue position
Fig. 5 shows Takizawa’s Rogue position.